PRUEBA DE HIPÓTESIS PARA COCIENTE DE VARIANZA

PRUEBA DE HIPÓTESIS PARA COCIENTE DE VARIANZAS

PEDRO GIL

En esta sección estudiaremos la prueba de hipótesis relacionada con varianzas o desviaciones estándar de la población. No son poco comunes las aplicaciones de pruebas de una y dos muestras sobre varianzas.

Los ingenieros y los científicos constantemente se enfrentan a estudios donde se les pide demostrar que las mediciones que tienen que ver con productos o procesos cumplen con las especificaciones que fijan los consumidores.

Las especificaciones a menudo se cumplen si la varianza del proceso es suficientemente pequeña. También existe interés por experimentos que comparan métodos o procesos donde la reproducibilidad o variabilidad inherentes se deben comparar de manera formal. Además, para determinar si no se cumple la suposición de varianzas iguales, con frecuencia se aplica una prueba que compara dos varianzas antes de llevar a cabo una prueba t sobre dos medias.

Empecemos por considerar el problema de probar la hipótesis nula H0  de que la varianza de la población 𝞼² es igual a un valor específico 𝞼²0 contra una de las alternativas comunes:

 

El estadístico apropiado sobre el que basamos nuestra decisión es el estadístico chi cuadrada.

Formalizamos esto en el siguiente teorema: 

Por lo tanto, si suponemos que la distribución de la población que se muestrea es normal, el valor de chi cuadrada para probar  𝞼² = 𝞼²0 es dado por:   

Los valores de la variable aleatoria X² se calculan de cada muestra mediante la anterior fórmula.

Donde n es el tamaño de la muestra, s²  Es la varianza muestral y 𝞼²0 Es el valor de 𝞼² dado por la hipótesis nula.

Si H0  es verdadera,  X² es un valor de la distribución chi cuadrada con v = n - 1 de libertad. 

En consecuencia, para una prueba de dos colas a un nivel de significancia α, la región crítica es: 

Para la alternativa unilateral: 𝞼² < 𝞼²0 La región crítica es:

;

y para la alternativa unilateral: 𝞼² > 𝞼²0 La región crítica es:

Robustez de la prueba X² (chi cuadrado) para la suposición de normalidad:

Varias pruebas dependen, al menos en teoría, de la suposición de normalidad.

En general muchos procedimientos en estadística aplicada tienen fundamentos teóricos que dependen de la distribución normal. Estos procedimientos varían en el grado en que dependen de la suposición de la normalidad. A un procedimiento que es razonablemente insensible a esta suposición se le denomina procedimiento robusto, es decir, robusto para la normalidad.

La prueba chi cuadrado sobre una sola varianza no es robusta en absoluto para la normalidad, es decir, el éxito práctico del procedimiento depende de la normalidad. Como resultado, el valor P  calculado podría ser notoriamente diferente del valor P verdadero si la población de la que se toma la muestra no es normal. De hecho, resulta muy plausible que un valor P estadísticamente significativo no sea una verdadera señal de:

sino que un valor significativo sea el resultado de haber violado las suposiciones de normalidad. Por lo tanto, el analista debería utilizar esta prueba específica con precaución.

EJEMPLO:

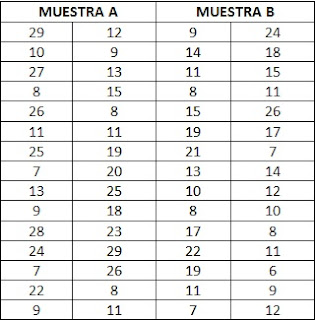
     Al probar la diferencia en el desgaste abrasivo de los dos materia les del ejemplo 10.6 supusimos que las dos varianzas de la población desconocidas eran iguales. ¿Se justifica tal suposición? Utilice un nivel de significancia de 0.10.

SOLUCIÓN: