REGIONES DE RECHAZO Y NO RECHAZO

REGIONES DE RECHAZO Y NO RECHAZO

JESSICA GARCÍA

Como se ha mencionado antes, en la práctica se tienen que tomar decisiones sobre poblaciones partiendo de la información muestral de las mismas y tales decisiones se llaman decisiones estadísticas. Por su parte, cualquier investigación implica la existencia de dos hipótesis o afirmaciones acerca de las poblaciones que se estudian, las cuales pueden ser o no ciertas y reciben el nombre de hipótesis estadísticas.

Las hipótesis estadísticas se divide en dos tipos: Hipótesis Nula (la cual se refiere siempre a un valor especificado del parámetro de población, no a una estadística de muestra y su planteamiento siempre contiene un signo de igualdad con respecto al valor especificado del parámetro) e Hipótesis Alternativa (la cual es cualquier hipótesis que difiera de la nula y su planteamiento nunca contiene un signo de igualdad con respecto al valor especificado del parámetro).

La distribución de muestreo de la estadística de prueba se divide en dos regiones:

     1) Región de Rechazo: Conocida como región crítica.

     2) Región de No Rechazo: Conocida como región de aceptación.

Si la estadística de prueba cae dentro de la región de aceptación, no se puede rechazar la hipótesis nula. Por otro lado, la región de rechazo puede considerarse como el conjunto de valores de la estadística de prueba que no tienen posibilidad de presentarse si la hipótesis nula es verdadera pero estos valores no son tan improbables de presentarse si la hipótesis nula es falsa. Igualmente el valor crítico separa la región crítica de la región de aceptación.

Cuando la hipótesis nula es rechazada cuando de hecho es verdadera y debía ser aceptada, se habla de un error tipo I pero cuando la hipótesis nula es aceptada cuando de hecho es falsa y debía ser rechazada, estaríamos hablando de un error tipo II. En conclusión, en cualquiera de los dos casos se comete un error al tomar una decisión equivocada.

EJEMPLO

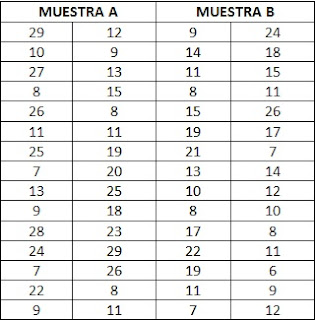
Se realiza un estudio acerca del impacto que tiene el Programa de Planificación Familiar de un hospital en dos asentamientos humanos de su jurisdicción, uno ubicado en el área urbana (A) y otro en el área rural (B), tomando para ello dos muestras de mujeres en edad fértil y con actividad sexual: nA = 30 y nB = 30. Después de aplicado el instrumento de medición, se obtienen los siguientes datos:

DATOS

Según los datos obtenidos y suponiendo normalidad, ¿podríamos decir que el impacto fue mayor en las mujeres del asentamiento humano ubicado en el área urbana? Utilizar un nivel de significación del 5%.

RESPUESTA

1) Planteamiento de Hipótesis:

     Ho: μ1 ≤ μ2

     H1: μ1 > μ2

2) Nivel de Significancia: α = 0.05

3) Prueba Estadística:

Con los supuestos de que las distribuciones son normales y de que las muestras se seleccionaron al azar.

4) Criterio de Decisión:

Si Zc ≤ 1,64; se acepta la Ho. En caso contrario se rechaza.

5) Cálculos:

6) Conclusiones:

   1) Se rechaza la hipótesis nula (Ho), se acepta la hipótesis alterna (H1) a un nivel de significancia de α = 0.05 y la prueba resultó ser significativa.

   2) La evidencia estadística no permite aceptar la hipótesis nula.

   3) La evidencia estadística disponible permite concluir que probablemente el impacto del Programa de Planificación Familiar fue mayor en las mujeres del asentamiento humano de área urbana.