PRUEBA DE HIPOTESIS PARA LA VARIANZA

-


PRUEBA DE HIPÓTESIS PARA LA VARIANZA

PEDRO GIL

    

  En situaciones como control estadístico de la calidad, de antemano se conocen los parámetros de referencia del proceso bajo control. La actividad central para decidir si en un momento dado, el proceso esta bajo control, es la confrontación permanente de los datos obtenidos con la hipótesis sobre la centralidad del proceso (media) y sobre la magnitud de su variabilidad (varianza). 

     La varianza como medida de dispersión es importante dado que nos ofrece una mejor visión de dispersión de datos.

     Si se desea probar una hipótesis acerca de la varianza se puede hacer utilizando las medidas estadísticas con las que se construyo el intervalo de confianza σ2, esto es con la distribución ji- cuadrada. Así podremos determinar una franja de confianza, con base en la cual podríamos tomarse decisiones al respecto.

     Para esto entonces debemos conocer nuestro estadístico de prueba considerando que la población sigue una distribución normal:


EJEMPLO:
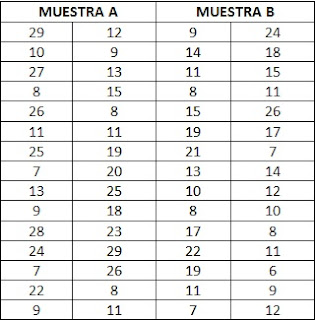
     Considerando que el arribo de un metrobus a la estación Plaza Venezuela es en promedio de 45 segundos y su variabilidad (varianza) debiera ser de 5 segundos. ¿Muestran los siguientes datos suficiente evidencia de que esta varianza ha cambiado? Use un α = 0.05 Tomamos el tiempo de una muestra periódica de 16 autobuses para controlar la periodicidad de arribo y se obtienen los siguientes datos en segundos:


SOLUCIÓN:

























CONCLUSIÓN: 

      La Hipótesis se acepta ya que se encuentra en la región de aceptación y podemos afirmar que nuestra variabilidad no ha cambiado de 5 segundos, pero se acerca mucho al valor critico y es complicado tomar una decisión.

Comentarios

  1. Michel N. Coppola11 de mayo de 2020 a las 11:07 a.m.

    Cuando se analizan variables cuantitativas, a menudo es importante sacar conclusiones en cuanto a la variabilidad así como al promedio de una característica de interés. Por ejemplo, en el estudio de las llantas, el gerente de la fábrica, probablemente se interesaría en determinar si la variabilidad en la duración de las llantas está o no dentro de los límites aceptables antes de concluir que el proceso funciona en forma correcta. En este caso, lo que interesaría sería llegar a conclusiones acerca de la desviación estándar o a la varianza de la población.

    Si se intenta llegar a conclusiones en cuanto a la variabilidad de la población, primero se debe determinar qué prueba estadística se puede usar para representar la distribución de la variabilidad en los datos de la muestra.

    ResponderBorrar
  2. Jessica García11 de mayo de 2020 a las 2:07 p.m.

    En el caso de la prueba de hipótesis para la varianza, si se extrae una muestra aleatoria de tamaño n de una población normal con media µ y varianza σ2, y se calcula la varianza muestral, se obtiene el valor del estadístico s2 que se utilizará para conocer la σ2, mediante una variable aleatoria chi cuadrada con “n-1” grados de libertad. Formalizando con el siguiente teorema: si s2 es la varianza de una muestra aleatoria de tamaño “n” que se toma de una población normal que tiene varianza σ2, entonces el estadístico tiene una distribución chi cuadrado con v = n-1, grados de libertad.

    ResponderBorrar

Publicar un comentario

Entradas más populares de este blog

REGIONES DE RECHAZO Y NO RECHAZO

-
Imagen
REGIONES DE RECHAZO Y NO RECHAZO JESSICA GARCÍA Como se ha mencionado antes, en la práctica se tienen que tomar decisiones sobre poblaciones partiendo de la información muestral de las mismas y tales decisiones se llaman decisiones estadísticas. Por su parte, cualquier investigación implica la existencia de dos hipótesis o afirmaciones acerca de las poblaciones que se estudian, las cuales pueden ser o no ciertas y reciben el nombre de hipótesis estadísticas. Las hipótesis estadísticas se divide en dos tipos: Hipótesis Nula (la cual se refiere siempre a un valor especificado del parámetro de población, no a una estadística de muestra y su planteamiento siempre contiene un signo de igualdad con respecto al valor especificado del parámetro) e Hipótesis Alternativa (la cual es cualquier hipótesis que difiera de la nula y su planteamiento nunca contiene un signo de igualdad con respecto al valor especificado del parámetro). La distribución de muestreo de la estadística d...
Leer más

PRUEBA DE HIPOTESIS (HP)

-
Imagen
PRUEBA DE HIPÓTESIS (HP) JESSICA GARCÍA Una Prueba de Hipótesis (HP) es un procedimiento con el que se busca tomar una decisión sobre el valor de verdad de una hipótesis estadística, es decir, el valor de una afirmación acerca de la distribución de una variable aleatoria. Al realizar dicha prueba, se decide si se rechaza o no esa hipótesis estadística y la decisión se basa en la evidencia muestral. Una manera más simplificada de verlo es el siguiente: Entender con exactitud qué es una Prueba de Hipótesis (HP) implica comprender muchos conceptos tanto como variable, parámetro, hipótesis estadística, estadístico de prueba, etc y las relaciones entre ellos. Pero la idea general del tema no es difícil de entender, de hecho es muy intuitivo. A continuación se presentará un ejemplo que expresa, de manera natural, el razonamiento y procedimiento detrás de una Prueba de Hipótesis (HP). EJEMPLO Un fabricante de galletas produce paquetes en los cuales el peso nomin...
Leer más

PRUEBA DE HIPÓTESIS PARA COCIENTE DE VARIANZA

-
Imagen
PRUEBA DE HIPÓTESIS PARA COCIENTE DE VARIANZAS PEDRO GIL En esta sección estudiaremos la prueba de hipótesis relacionada con varianzas o desviaciones estándar de la población. No son poco comunes las aplicaciones de pruebas de una y dos muestras sobre varianzas. Los ingenieros y los científicos constantemente se enfrentan a estudios donde se les pide demostrar que las mediciones que tienen que ver con productos o procesos cumplen con las especificaciones que fijan los consumidores. Las especificaciones a menudo se cumplen si la varianza del proceso es suficientemente pequeña. También existe interés por experimentos que comparan métodos o procesos donde la reproducibilidad o variabilidad inherentes se deben comparar de manera formal. Además, para determinar si no se cumple la suposición de varianzas iguales, con frecuencia se aplica una prueba que compara dos varianzas antes de llevar a cabo una prueba  t  sobre dos medias. Empecemos por c...
Leer más